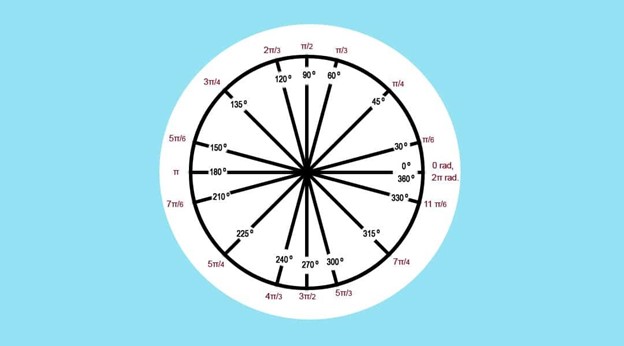
In mathematics, such a definition as an angle is measured in degrees and radians.

These two angle measurements have a connection, and it is necessary to unquestionably understand what it is. Comprehending and clarifying this connection permits you to work with angles and convert degrees to radians and from radians to degrees.

In this material, we will try to understand and derive the basic formula for how to convert degrees to radians in the value of radians and, accordingly, in the reverse order.

The history of these terms

Both metrics are branches of angle. They are rehearsed in math, physics, engineering, and other applied sciences. The history of the degree goes back to archaic Babylonian records, but the radian is a fairly current idea presented in 1714 by Roger Cotes. The degree is generally operated elemental unit for measuring angle. Although it is the most typical unit of measure in technique.

Invented degrees in ancient Babylon. How? Very simple! They just took it and broke the circle into 360 equal pieces. Why exactly 360? Not 100 or 1000? It seems that the number 100 is more equal to 360. That is a good query. The main version is astronomical. After all, 360 is very immediate to the number of days a year! And for observing the Sun, Moon, and stars, it was very convenient. In addition, in astronomy (as well as construction, surveying, and other related fields) it is very convenient to divide the circle into equal parts. And now let's estimate purely mathematically, by which number is 100 completely divisible and by which - 360? And in which of the variants of these divisors is it more? And for people, such a division is very convenient.

In addition, in astronomy (as well as building, surveying, and other connected areas) it is very suitable to separate the circle into equal parts.

What is essential?

Degrees take their position in our lives. We must know how much we need to turn the telescope, the snowboard around, or the steering wheel. According to the laws of nature, we observe how others move. And radians are more suitable for those who move than those who observe them. You need to understand:

The degrees are arbitrarily chosen as they are established on the sun, while they seem to go back because they describe processes from the viewer's pinpoint.

Radians describe the movement from the perspective of its participants, and therefore "everything falls into place." Transforming angular velocity to unbent velocity is straightforward, and concepts like sin(x)/x make significance.

Actually angles may be viewed from more than one perspective. Comprehending radians makes mathematical and physical formulas more meaningful.

Radians

Along with degrees, other units of measure are often operated - radians (from Latin radii - radius). It is a more appropriate unit for round bodies because it is directly related to their geometry. So, one radian is an angle that relies on the length of the arc of a circle, equal to its radius. Since the circumference is calculated by the formula L = 2piR, where pi is pi equal to 3.14, then the full circle is 2pi radians. Measuring angles in radians is very convenient in trigonometry, where calculations and transformations of trigonometric functions are performed in this particular calculation system. For example, sin(pi/2) = 1.